문제
https://school.programmers.co.kr/learn/courses/30/lessons/92343
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
- 소요 시간 : 1시간
- 난이도 : LV 2
나의 풀이
접근 방법
1. 노드별로 루트까지 가면서 들러야 하는 늑대의 개수를 체크한다.
2. 개수가 적은대로 방문한다.
시간복잡도
for : O(N) * go_to_root : O(N) = O(N^2)
코드
def solution(info, edges):
answer = 0
childs = [[] for i in range(len(info))]
parents = [0 for i in range(len(info))]
visited = [False for i in range(len(info))]
for parent, child in edges:
childs[parent].append(child)
parents[child] = parent
def get_wolfs (n: int, wolfs: int):
if n == 0:
return wolfs
if info[n]:
wolfs += 1
return get_wolfs(parents[n], wolfs)
def go_to_root(n: int, wolfs: int, sheeps: int):
if not visited[n]:
if info[n]:
wolfs += 1
else:
sheeps += 1
if wolfs == sheeps:
sheeps = 0
visited[n] = True
if n == 0:
return (wolfs, sheeps)
else:
return go_to_root(parents[n], wolfs, sheeps)
# 양별 늑대 개수
sheeps = []
for i in range(len(info)):
if not info[i]:
sheeps.append((i, get_wolfs(i, 0)))
sheeps.sort(key = lambda x :(x[1], x[0]))
# 방문
wolf_cnt = 0
sheep_cnt = 0
curr = 0
# 최소 공통 조상 ..
for dest, wolfs in sheeps:
# 이동
# 루트 -> 현재
wolf_cnt, sheep_cnt = go_to_root(curr, wolf_cnt, sheep_cnt)
print(f"curr : {curr} -> root = ", "wolf : ", wolf_cnt, "sheep : ", sheep_cnt)
# 루트 -> 목적지
wolf_cnt, sheep_cnt = go_to_root(dest, wolf_cnt, sheep_cnt)
print(f"dest : {dest} -> root = ", "wolf : ", wolf_cnt, "sheep : ", sheep_cnt)
print("=====")
curr = dest
answer = max(answer, sheep_cnt)
print(sheeps)
return answer
결과 : 실패
실패 요인
방문하는 과정에서 현재 -> 루트 -> 목적지로 가는 과정을 어떻게 구현할지 고민하다가
(현재 -> 루트) + (목적지 -> 루트) 로 구현했는데,
목적지 -> 루트로 가게 되어 순서가 뒤바뀌어버려서 늑대와 양이 동일한 개수가 정확하지 않다.
아래 그림을 예시로 들면
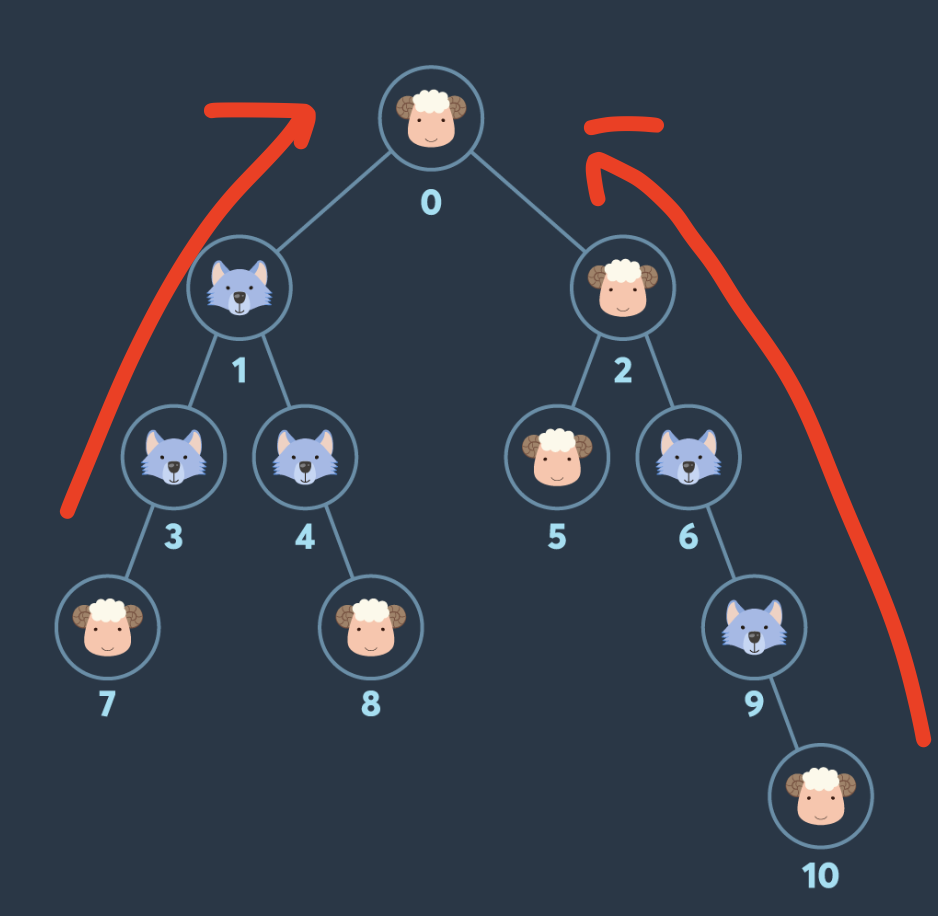
0번, 2번, 5번, 7번, 8번을 방문하면 양이 5마리, 늑대가 2마리인 상태에서
다음 목적지인 10번으로 방문할 때 나의 로직은 아래와 같다.
8 -> 0 = 양 5, 늑대 3
10 -> 0 = 양 6, 늑대 5
10 방문 : 양 6, 늑대 3
10 -> 9: 양 6, 늑대 4
9 -> 6: 양 6, 늑대 5
6 -> 2 : 양 6 (이미 방문), 늑대 5
2 -> 0 : 양 6, 늑대 5
0 -> 10 순서로 가야 양 5, 늑대 5가 되면서 잡아먹히는데 내 로직에 오류가 있는 것이다.
다른 사람의 풀이
[프로그래머스 L3] 양과 늑대 (python)
2022 KAKAO BLIND RECRUITMENT > (L3) 양과 늑대각 노드에 있는 양 또는 늑대에 대한 정보가 담긴 배열 info, 2진 트리의 각 노드들의 연결 관계를 담은 2차원 배열 edges가 매개변수로 주어질 때, 문제에 제시
velog.io
접근 방법
- 양의 수가 늑대의 수보다 많은지?
- 부모 노드를 방문한 적이 있는지? 자식 노드는 처음 방문하는지?
위의 두 조건을 이용해서 DFS + 백트래킹을 이용한다.
1. 양이 늑대보다 많으면 양의 수를 결과 배열에 저장해둔다. (단, 양이 늑대보다 같거나 적으면 해당 과정을 끝낸다.)
2. edge 배열을 돌면서 방문된 부모 노드와 방문되지 않은 자식 노드 정보가 있으면
2-1. 자식 노드에 방문 처리를 해준다.
2-2. 양 또는 늑대 수를 업데이트한다.
2-3. 계속 반복한다.
위 과정이 끝나면, 양의 수를 저장한 배열에서의 최댓값이 모을 수 있는 양의 최대 수가 된다.
시간복잡도
DFS 탐색이 모든 노드에 대해 발생하며, 각 노드에서 간선 리스트를 확인하므로 O(N * M)이다.
N: 노드의 수 (총 info 리스트의 길이)
M: 간선의 수 (총 edges 리스트의 길이)
코드
def solution(info, edges):
visited = [False] * len(info)
answer = []
def dfs(sheep, wolf):
if sheep > wolf:
answer.append(sheep)
else:
return
for p, c in edges:
if visited[p] and not visited[c]:
visited[c] = True
if info[c]:
dfs(sheep, wolf+1)
else:
dfs(sheep+1, wolf)
visited[c] = False
# 루트 노드부터 시작
visited[0] = True
dfs(1, 0)
return max(answer)
결과 : 정답
| 테스트 1 〉 | 통과 (0.01ms, 10.2MB) |
| 테스트 2 〉 | 통과 (0.21ms, 10.2MB) |
| 테스트 3 〉 | 통과 (0.01ms, 10.2MB) |
| 테스트 4 〉 | 통과 (0.01ms, 9.99MB) |
| 테스트 5 〉 | 통과 (0.35ms, 10.1MB) |
| 테스트 6 〉 | 통과 (0.18ms, 10.1MB) |
| 테스트 7 〉 | 통과 (0.05ms, 10.2MB) |
| 테스트 8 〉 | 통과 (0.04ms, 10.1MB) |
| 테스트 9 〉 | 통과 (0.56ms, 10.1MB) |
| 테스트 10 〉 | 통과 (8.67ms, 10MB) |
| 테스트 11 〉 | 통과 (0.22ms, 10.3MB) |
| 테스트 12 〉 | 통과 (1.02ms, 10.4MB) |
| 테스트 13 〉 | 통과 (0.04ms, 10.1MB) |
| 테스트 14 〉 | 통과 (0.09ms, 10.2MB) |
| 테스트 15 〉 | 통과 (0.71ms, 10.2MB) |
| 테스트 16 〉 | 통과 (1.13ms, 10.2MB) |
| 테스트 17 〉 | 통과 (11.51ms, 10.4MB) |
| 테스트 18 〉 | 통과 (0.32ms, 10.3MB) |
위 풀이도 깔끔하고 좋았지만 매번 edges를 탐색하는 게 비효율적이라고 생각되어 다른 풀이를 찾아보았다.
다른 사람의 풀이
https://school.programmers.co.kr/questions/25736
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
접근 방법
DFS + 완전탐색을 이용한다.
이미 지나갔던 정점은 생각해봤을 때, 다시 방문하더라도,
아무런 변화가 없습니다. 왜냐하면 최초방문시에 해다 정점에 서식했던 동물이 따라오게 때문이고,
그게 게임이 끝날 때 까지 계속 따라 다니기 때문입니다. 같은 정점을 다시 방문해도 결국에는, 아무런 의미가 없습니다.
부모 정점을 방문하여 이미 길이 만들어졌으면,
그 부모 정점의 하나 바로 밑에 존재하는 자식 정점들은 언제든지 입장이 가능하게 됩니다.
모든 그래프를 전부 방문하게 되면 자연스럽게 다음에 방문할 수 있는 그래프가 존재하지 않게 되므로,
재귀호출이 일어나지 않습니다.
0. 결과를 저장할 변수를 초기화한다.
1. 인접리스트로 graph[부모] = [자식 리스트]를 만든다.
2. (현재 정점, 양의 수, 늑대의 수, 이동가능한 정점들)을 인자로 한 dfs함수를 만든다.
2-1. 현재 정점이 늑대인지 양인지에 따라 양 또는 늑대의 카운트를 하나 올린다.
2-2. (결과를 저장하는 변수 < 양의 수) 이면 결과변수 = 양의 수 로 값을 업데이트한다.
2-3. 만약 (늑대의 수 >= 양의 수) 이면 리턴 한다. 더 이상 수행하면 답을 구할 수 없기 때문이다.
2-4. 이동가능한 정점 리스트에 현재 정점의 자식 정점들을 추가한다.
현재 정점을 방문했기 때문에, 현재 정점의 자식 정점들을 탐색할 수 있는 권한이 주어졌기 때문이다. 길이 뚫린 것이다.
2-5. for문으로 이동가능한 정점들을 탐색하면서, 하나씩 해당 정점을 새로운 이동가능한 정점에서 제거하여, 다음 재귀호출을 진행한다.
ex. 이동 가능한 정점이 [1,8]이라고 가정할 때, for문은 1과 8을 각각 탐색하게 된다.
1을 탐색할 경우, dfs로 재귀 호출을 할 때 현재 정점은 1이 되고, 이동 가능한 정점은 [8] 이 된다.
그 후 8을 탐색하게 되면, 재귀 호출 시 현재 정점은 8이 되고, 이동 가능한 정점은 [1]이 된다.
* for문의 역할은 이동 가능한 정점을 하나씩 순회하여 모든 경우의 수를 탐색하는 것이다.
해당 정점을 탐색할 때 그 정점은 현재 정점이 되며, 이미 방문했기 때문에 재방문을 방지하기 위해 이동 가능한 정점에서 자기 자신을 제거한다.
단방향 그래프이므로, 같은 정점을 다시 방문하지 않게 되어 시간 복잡도를 획기적으로 줄일 수 있다.
3. 결과를 저장할 변수를 리턴한다.
주의할 점
- 이동 가능한 정점은 리스트 형태로 재귀 호출 시, 리스트의 복사가 완전히 이루어지지 않으면 독립적인 변수로 취급되지 않으며, 다른 곳에서 값이 변경되면 연쇄적으로 영향을 받을 수 있다. 따라서, 배열이나 리스트의 값을 독립적으로 수정할 때는 항상 복제를 해 독립적인 리스트로 사용해야 한다.
- 결과 변수의 최대값 갱신은 양과 늑대의 수를 업데이트한 이후, 늑대 수가 양 수를 초과하는 조건문을 확인하는 과정에서 이루어져야 한다. 늑대가 양의 수를 따라잡거나 초과하는 조건문에서만 최대값을 갱신하면, 모든 정점을 탐색하는 과정에서 양의 수가 늑대의 수보다 많은 경우를 올바르게 탐색할 수 없게 된다.
시간복잡도
O(2^N) : 각 노드에서 가능한 경로들이 계속 확장되며, 모든 가능한 상태를 탐색할 수 있다.
하지만 실제 동작에서는 경로가 제한되기 때문에 모든 경로를 다 탐색하지는 않겠지만, 이론적으로는 지수 복잡도를 가질 수 있다.
코드
from collections import defaultdict
def solution(info, edges):
graph = defaultdict(list)
# 그래프 구성
for parent, child in edges:
graph[parent].append(child)
# DFS 정의
def dfs(node, sheep, wolf, possible_nodes):
nonlocal answer
if info[node] == 0:
sheep += 1
else:
wolf += 1
# print("=======")
# print("node : ", node)
# print("sheep : ", sheep, " wolf : ", wolf)
# print(possible_nodes)
# 늑대가 양을 넘으면 더 이상 탐색하지 않음
if wolf >= sheep:
return
# 최대 양의 수 갱신
answer = max(answer, sheep)
# 이동 가능한 노드 복제 (다른 경로에 영향 안 미치도록)
nodes = possible_nodes[:]
nodes.remove(node)
nodes.extend(graph[node])
# print(nodes)
# 다음 가능한 정점들로 이동
for next_node in nodes:
dfs(next_node, sheep, wolf, nodes)
answer = 0
dfs(0, 0, 0, [0]) # 시작은 0번 정점
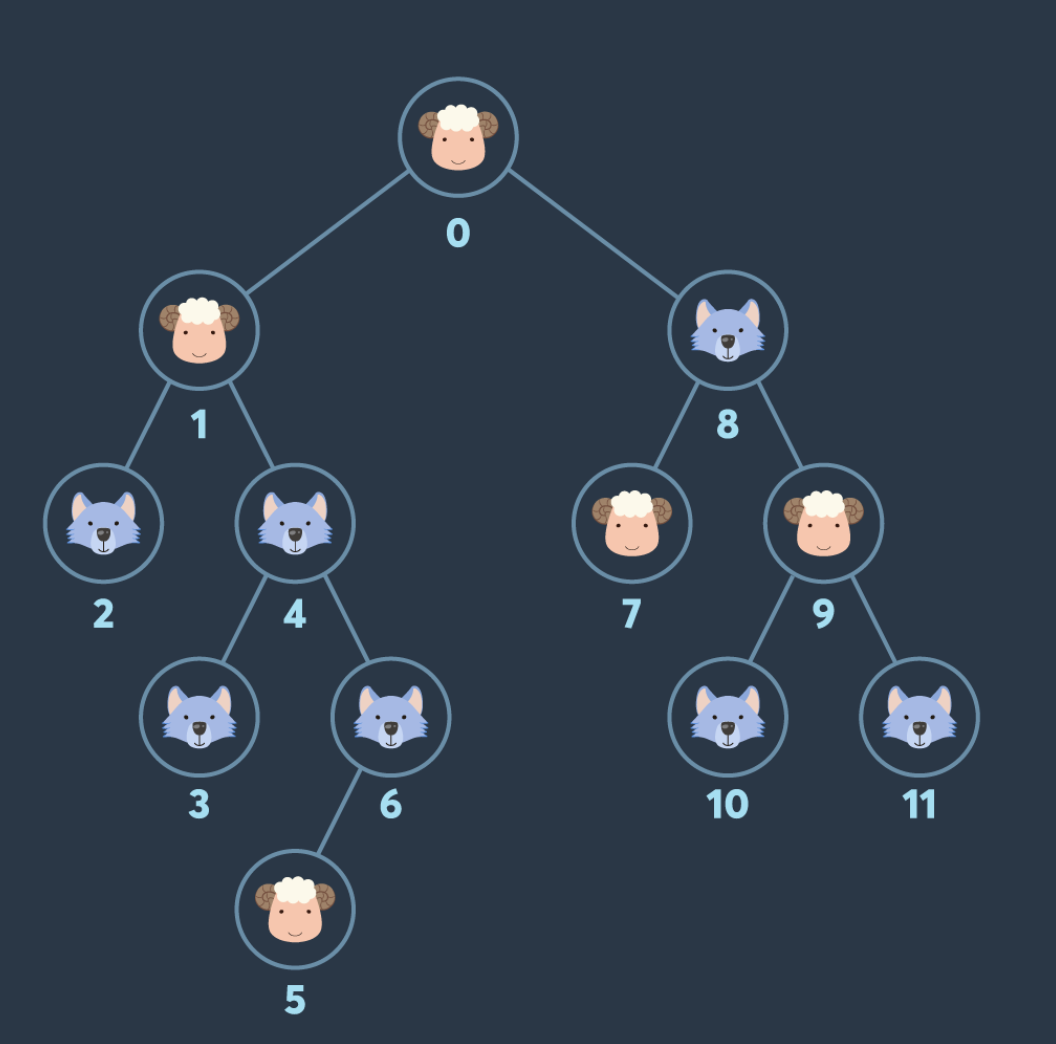
return answer어떻게 DFS가 되는지 print로 찍은 로그로만으로는 잘 이해가 안가서 직접 적어보았다.
너무 길어서 다는 못했지만 어떻게 DFS가 되는지 확실히 이해가 갔다.

결과 : 정답
| 테스트 1 〉 | 통과 (0.01ms, 10.1MB) |
| 테스트 2 〉 | 통과 (0.09ms, 10.3MB) |
| 테스트 3 〉 | 통과 (0.01ms, 10.1MB) |
| 테스트 4 〉 | 통과 (0.01ms, 10.2MB) |
| 테스트 5 〉 | 통과 (0.20ms, 10.1MB) |
| 테스트 6 〉 | 통과 (0.14ms, 10.2MB) |
| 테스트 7 〉 | 통과 (0.05ms, 10.2MB) |
| 테스트 8 〉 | 통과 (0.05ms, 10.2MB) |
| 테스트 9 〉 | 통과 (0.40ms, 10.2MB) |
| 테스트 10 〉 | 통과 (2.72ms, 10.1MB) |
| 테스트 11 〉 | 통과 (0.15ms, 10.3MB) |
| 테스트 12 〉 | 통과 (0.63ms, 10.2MB) |
| 테스트 13 〉 | 통과 (0.03ms, 10.2MB) |
| 테스트 14 〉 | 통과 (0.07ms, 10.2MB) |
| 테스트 15 〉 | 통과 (0.25ms, 10MB) |
| 테스트 16 〉 | 통과 (0.38ms, 10.2MB) |
| 테스트 17 〉 | 통과 (7.33ms, 10.2MB) |
| 테스트 18 〉 | 통과 (0.24ms, 10MB) |
정리
DFS에 조금 약하다고 생각했는데 드러난 문제..
다시 풀어봐야겠다.
'코딩테스트' 카테고리의 다른 글
| [프로그래머스] 연속 펄스 부분 수열의 합 - Python (0) | 2024.10.18 |
|---|---|
| [프로그래머스] 숫자 변환하기 - Python (0) | 2024.10.18 |
| [프로그래머스] 무인도 여행 - Python (1) | 2024.10.16 |
| [프로그래머스] 미로 탈출 명령어 - Python (1) | 2024.10.16 |
| [프로그래머스] 뒤에 있는 큰 수 찾기 - Python (2) | 2024.10.15 |
