비교 방식 알고리즘 (Comparisons Sorting Algorithm)
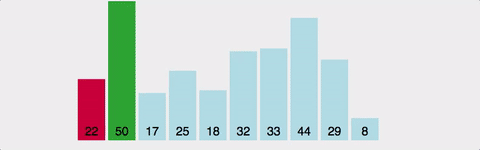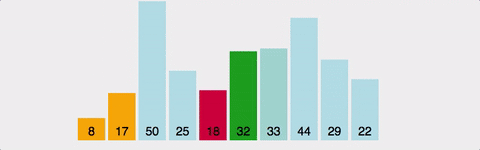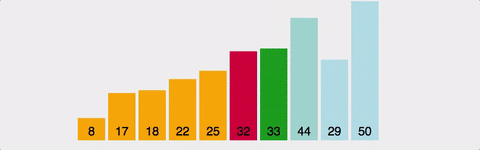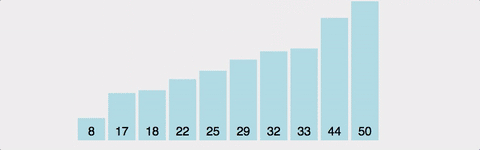
선택 정렬 (Selection Sort)
가장 작은 값을 배열의 맨 앞에다 이동시키면서 정렬한다.
| 시간복잡도 | 공간복잡도 |
| O(N^2) | O(1) |
코드
li = [5, 2, 4, 3, 1]
for i in range(len(li)-1):
min_idx = i
for j in range(i+1, len(li)):
if li[min_idx] > li[j]:
min_idx = j
li[i], li[min_idx] = li[min_idx], li[i]
print(li)
>>> [1, 2, 4, 3, 5]
>>> [1, 2, 4, 3, 5]
>>> [1, 2, 3, 4, 5]
>>> [1, 2, 3, 4, 5]버블 정렬 (Bubble Sort)
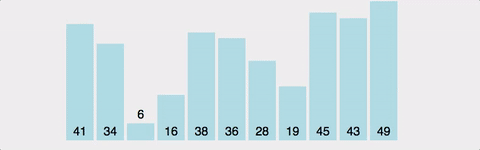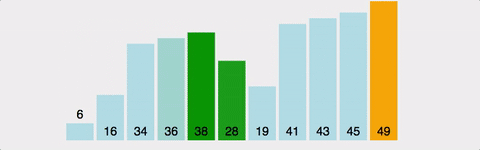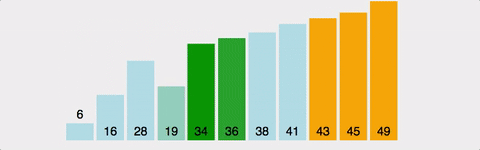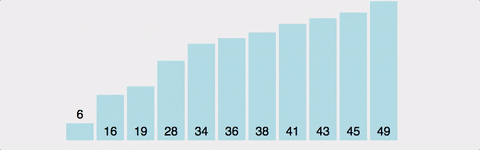
인접한 두 개의 데이터를 비교해가면서 정렬을 진행하는 방식이다.
가장 큰 값을 배열의 맨 끝에다 이동시키면서 정렬한다.
| 시간복잡도 | 공간복잡도 |
| O(N^2) | O(1) |
코드
li = [5, 2, 4, 3, 1]
for i in range(len(li)-1, 0, -1):
for j in range(i):
if li[j] > li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
print(li)
>>> [2, 4, 3, 1, 5]
>>> [2, 3, 1, 4, 5]
>>> [2, 1, 3, 4, 5]
>>> [1, 2, 3, 4, 5]
삽입 정렬 (Insertion Sort)
버블정렬의 비효율성을 개선하기 위해 등장했다.
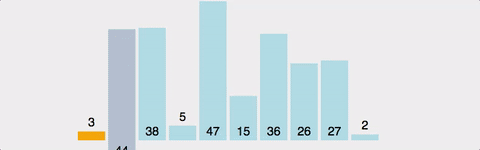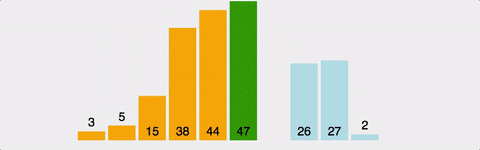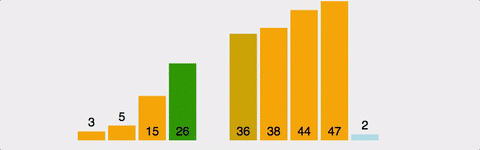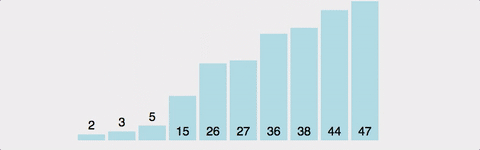
현재 위치에서 그 이하의 배열들을 비교해 자신이 들어갈 위치를 찾아 그 위치에 삽입하여 정렬한다.
비교하는 원소보다 자신이 클 경우 서로의 위치를 바꾸고, 작을 경우 위치를 바꾸지 않고 다음 순서의 원소와 비교하면서 정렬해준다.
이 과정을 정렬하려는 배열의 마지막 원소까지 반복해준다.
n번 진행했을 경우 n+1번째까지 정렬되어 있다.
| 시간복잡도 | 공간복잡도 | |
| 최악 | 역으로 정렬된 경우 | |
| O(N^2) | O(1) |
코드
for end in range(1, len(li)):
for i in range(end, 0, -1):
if li[i-1] > li[i]:
li[i-1], li[i] = li[i], li[i-1]
print(li)
>>> [2, 5, 4, 3, 1]
>>> [2, 4, 5, 3, 1]
>>> [2, 3, 4, 5, 1]
>>> [1, 2, 3, 4, 5]병합 정렬 (Merge Sort)
주어진 배열을 원소가 하나 밖에 남지 않을 때까지 계속 둘로 쪼갠 후에 다시 크기 순으로 재배열 하면서 원래 크기의 배열로 합친다.
분할하여 정복하는 알고리즘이다.
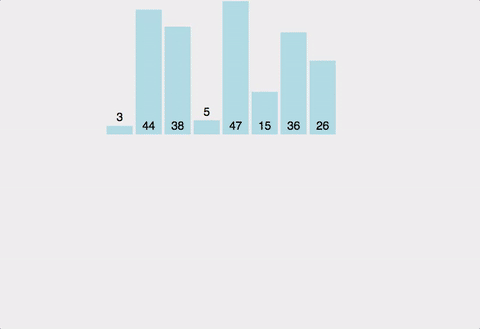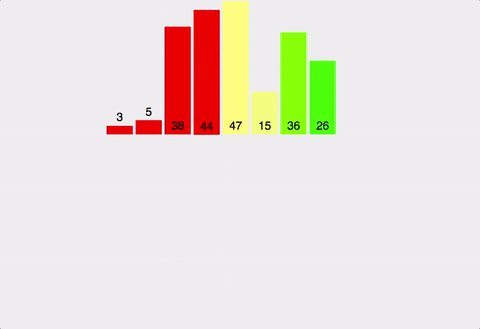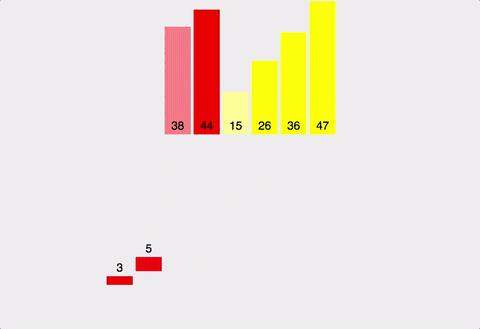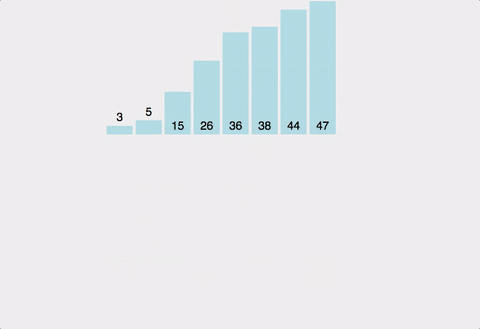
| 시간복잡도 | 공간복잡도 |
| O(NlogN) | O(N) |
시간복잡도 : 전반적인 반복의 수는 점점 절반으로 줄어들 기 때문에 O(logN) * 각 패스에서 병합할 때 모든 값들을 비교해야 하므로 O(N)
공간복잡도 : 두 개의 배열을 병합할 때 병합 결과를 담아 놓을 배열이 추가로 필요 O(N)
코드
def merge_sort(arr):
if len(arr) < 2:
return arr
mid = len(arr) // 2
low_arr = merge_sort(arr[:mid])
high_arr = merge_sort(arr[mid:])
print("====")
print(low_arr, high_arr)
merged_arr = []
l = h = 0
# 양쪽 모두 원소가 있는 상태에서 배열을 합친다.
while l < len(low_arr) and h < len(high_arr):
if low_arr[l] < high_arr[h]:
merged_arr.append(low_arr[l])
l += 1
else:
merged_arr.append(high_arr[h])
h += 1
# 아직 원소가 남은 배열에 있는 값을 복사한ㄴ다.
merged_arr += low_arr[l:]
merged_arr += high_arr[h:]
print(merged_arr)
return merged_arr
li = [5, 2, 4, 3, 1]
merge_sort(li)
>>> ====
>>> [5] [2]
>>> [2, 5]
>>> ====
>>> [3] [1]
>>> [1, 3]
>>> ====
>>> [4] [1, 3]
>>> [1, 3, 4]
>>> ====
>>> [2, 5] [1, 3, 4]
>>> [1, 2, 3, 4, 5]
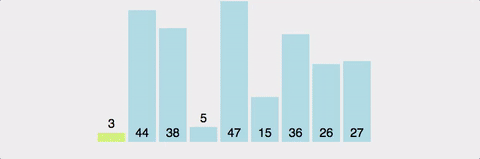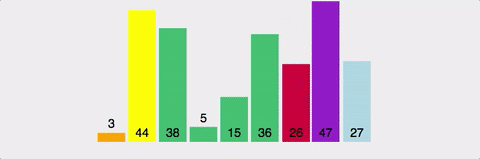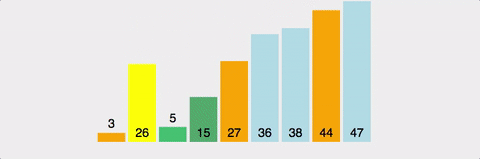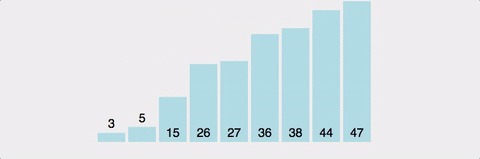
퀵 정렬 (Quick Sort)
pivot 값을 설정하고 이를 기준으로 한 부분집합에는 pivot보다 작은 값, 다른 부분집합에는 pivot보다 큰 값을 넣는다.
더 이상 쪼갤 부분집합이 없을 때까지 재귀로 반복한다.
마찬가지로 분할 정복 알고리즘이다.
| 시간복잡도 | 공간복잡도 | |
| 최선 | O(NlogN) | O(N) |
| 최악 | O(N^2) |
시간복잡도 : 어떤 pivot 값을 고르냐에 따라 성능이 결정된다.
- 이상적인 경우에는 pivot 값을 기준으로 동일한 개수의 작은 값들과 큰 값들이 분할되어 병합 정렬과 마찬가지로 O(nlog(n))이다.
- pivot 값을 기준으로 분할했을 때 값들이 한 편으로 크게 치우치게 되면, 퀵 정렬은 성능은 저하되게 되며, 최악의 경우 한 편으로만 모든 값이 몰리게 되어 O(n^2)의 시간 복잡도를 보이게 됩니다.
공간복잡도 : 퀵 정렬은 공간 복잡도는 구현 방법에 따라 달라질 수 있는데, 입력 배열이 차지하는 메모리만을 사용하는 in-place sorting 방식으로 구현을 사용할 경우, O(log(n))의 공간 복잡도를 가진 코드의 구현이 가능하다.
코드
def quicksort(arr):
if len(arr) < 2:
return arr
pivot = arr[len(arr) // 2]
left, equal, right = [], [], []
for i in arr:
if i > pivot:
right.append(i)
elif i < pivot:
left.append(i)
else:
equal.append(i)
print(left, equal, right)
return quicksort(left) + [pivot] + quicksort(right)
li = [5, 2, 4, 3, 1]
print(quicksort(li))
>>> [2, 3, 1] [4] [5]
>>> [2, 1] [3] []
>>> [] [1] [2]
>>> [1, 2, 3, 4, 5]
그 외 힙 정렬 (Heap Sort), 쉘 정렬 (Shell Sort), 기수 정렬 (Radix Sort) 등이 있다.
비교
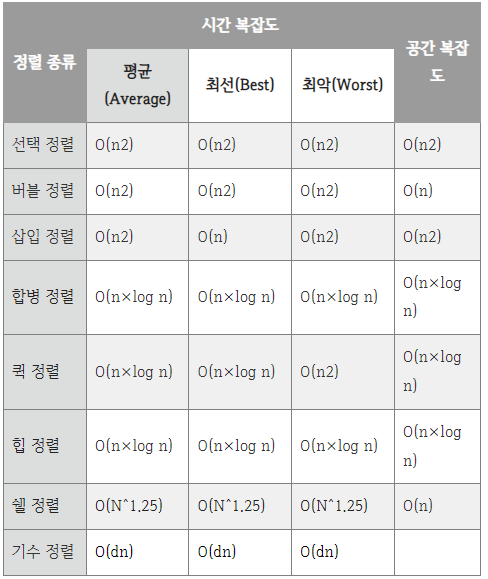

참고/
https://velog.io/@youhyeoneee/Sorting%EC%A0%95%EB%A0%AC
Sorting(정렬)
n개의 숫자가 입력으로 주어졌을 때, 이를 기준에 맞게 정렬하여 출력하는 알고리즘정렬 알고리즘에는 다양한 종류가 있고, 이에 따라 수행 시간도 다양하다.순차적으로 기준에 따라 현재 위치
velog.io
https://github.com/JaeYeopHan/Interview_Question_for_Beginner/tree/main/Algorithm
Interview_Question_for_Beginner/Algorithm at main · JaeYeopHan/Interview_Question_for_Beginner
:boy: :girl: Technical-Interview guidelines written for those who started studying programming. I wish you all the best. :space_invader: - JaeYeopHan/Interview_Question_for_Beginner
github.com
비교 방식 알고리즘 (Comparisons Sorting Algorithm)
선택 정렬 (Selection Sort)
가장 작은 값을 배열의 맨 앞에다 이동시키면서 정렬한다.

| 시간복잡도 | 공간복잡도 |
| O(N^2) | O(1) |
코드
li = [5, 2, 4, 3, 1]
for i in range(len(li)-1):
min_idx = i
for j in range(i+1, len(li)):
if li[min_idx] > li[j]:
min_idx = j
li[i], li[min_idx] = li[min_idx], li[i]
print(li)
>>> [1, 2, 4, 3, 5]
>>> [1, 2, 4, 3, 5]
>>> [1, 2, 3, 4, 5]
>>> [1, 2, 3, 4, 5]버블 정렬 (Bubble Sort)
인접한 두 개의 데이터를 비교해가면서 정렬을 진행하는 방식이다.
가장 큰 값을 배열의 맨 끝에다 이동시키면서 정렬한다.

| 시간복잡도 | 공간복잡도 |
| O(N^2) | O(1) |
코드
li = [5, 2, 4, 3, 1]
for i in range(len(li)-1, 0, -1):
for j in range(i):
if li[j] > li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
print(li)
>>> [2, 4, 3, 1, 5]
>>> [2, 3, 1, 4, 5]
>>> [2, 1, 3, 4, 5]
>>> [1, 2, 3, 4, 5]
삽입 정렬 (Insertion Sort)
버블정렬의 비효율성을 개선하기 위해 등장했다.
현재 위치에서 그 이하의 배열들을 비교해 자신이 들어갈 위치를 찾아 그 위치에 삽입하여 정렬한다.
비교하는 원소보다 자신이 클 경우 서로의 위치를 바꾸고, 작을 경우 위치를 바꾸지 않고 다음 순서의 원소와 비교하면서 정렬해준다.
이 과정을 정렬하려는 배열의 마지막 원소까지 반복해준다.
n번 진행했을 경우 n+1번째까지 정렬되어 있다.

| 시간복잡도 | 공간복잡도 | |
| 최악 | 역으로 정렬된 경우 | |
| O(N^2) | O(1) |
코드
for end in range(1, len(li)):
for i in range(end, 0, -1):
if li[i-1] > li[i]:
li[i-1], li[i] = li[i], li[i-1]
print(li)
>>> [2, 5, 4, 3, 1]
>>> [2, 4, 5, 3, 1]
>>> [2, 3, 4, 5, 1]
>>> [1, 2, 3, 4, 5]병합 정렬 (Merge Sort)
주어진 배열을 원소가 하나 밖에 남지 않을 때까지 계속 둘로 쪼갠 후에 다시 크기 순으로 재배열 하면서 원래 크기의 배열로 합친다.
분할하여 정복하는 알고리즘이다.

| 시간복잡도 | 공간복잡도 |
| O(NlogN) | O(N) |
시간복잡도 : 전반적인 반복의 수는 점점 절반으로 줄어들 기 때문에 O(logN) * 각 패스에서 병합할 때 모든 값들을 비교해야 하므로 O(N)
공간복잡도 : 두 개의 배열을 병합할 때 병합 결과를 담아 놓을 배열이 추가로 필요 O(N)
코드
def merge_sort(arr):
if len(arr) < 2:
return arr
mid = len(arr) // 2
low_arr = merge_sort(arr[:mid])
high_arr = merge_sort(arr[mid:])
print("====")
print(low_arr, high_arr)
merged_arr = []
l = h = 0
# 양쪽 모두 원소가 있는 상태에서 배열을 합친다.
while l < len(low_arr) and h < len(high_arr):
if low_arr[l] < high_arr[h]:
merged_arr.append(low_arr[l])
l += 1
else:
merged_arr.append(high_arr[h])
h += 1
# 아직 원소가 남은 배열에 있는 값을 복사한ㄴ다.
merged_arr += low_arr[l:]
merged_arr += high_arr[h:]
print(merged_arr)
return merged_arr
li = [5, 2, 4, 3, 1]
merge_sort(li)
>>> ====
>>> [5] [2]
>>> [2, 5]
>>> ====
>>> [3] [1]
>>> [1, 3]
>>> ====
>>> [4] [1, 3]
>>> [1, 3, 4]
>>> ====
>>> [2, 5] [1, 3, 4]
>>> [1, 2, 3, 4, 5]
퀵 정렬 (Quick Sort)
pivot 값을 설정하고 이를 기준으로 한 부분집합에는 pivot보다 작은 값, 다른 부분집합에는 pivot보다 큰 값을 넣는다.
더 이상 쪼갤 부분집합이 없을 때까지 재귀로 반복한다.
마찬가지로 분할 정복 알고리즘이다.

| 시간복잡도 | 공간복잡도 | |
| 최선 | O(NlogN) | O(N) |
| 최악 | O(N^2) |
시간복잡도 : 어떤 pivot 값을 고르냐에 따라 성능이 결정된다.
- 이상적인 경우에는 pivot 값을 기준으로 동일한 개수의 작은 값들과 큰 값들이 분할되어 병합 정렬과 마찬가지로 O(nlog(n))이다.
- pivot 값을 기준으로 분할했을 때 값들이 한 편으로 크게 치우치게 되면, 퀵 정렬은 성능은 저하되게 되며, 최악의 경우 한 편으로만 모든 값이 몰리게 되어 O(n^2)의 시간 복잡도를 보이게 됩니다.
공간복잡도 : 퀵 정렬은 공간 복잡도는 구현 방법에 따라 달라질 수 있는데, 입력 배열이 차지하는 메모리만을 사용하는 in-place sorting 방식으로 구현을 사용할 경우, O(log(n))의 공간 복잡도를 가진 코드의 구현이 가능하다.
코드
def quicksort(arr):
if len(arr) < 2:
return arr
pivot = arr[len(arr) // 2]
left, equal, right = [], [], []
for i in arr:
if i > pivot:
right.append(i)
elif i < pivot:
left.append(i)
else:
equal.append(i)
print(left, equal, right)
return quicksort(left) + [pivot] + quicksort(right)
li = [5, 2, 4, 3, 1]
print(quicksort(li))
>>> [2, 3, 1] [4] [5]
>>> [2, 1] [3] []
>>> [] [1] [2]
>>> [1, 2, 3, 4, 5]
그 외 힙 정렬 (Heap Sort), 쉘 정렬 (Shell Sort), 기수 정렬 (Radix Sort) 등이 있다.
비교


참고/
https://velog.io/@youhyeoneee/Sorting%EC%A0%95%EB%A0%AC
Sorting(정렬)
n개의 숫자가 입력으로 주어졌을 때, 이를 기준에 맞게 정렬하여 출력하는 알고리즘정렬 알고리즘에는 다양한 종류가 있고, 이에 따라 수행 시간도 다양하다.순차적으로 기준에 따라 현재 위치
velog.io
https://github.com/JaeYeopHan/Interview_Question_for_Beginner/tree/main/Algorithm
Interview_Question_for_Beginner/Algorithm at main · JaeYeopHan/Interview_Question_for_Beginner
:boy: :girl: Technical-Interview guidelines written for those who started studying programming. I wish you all the best. :space_invader: - JaeYeopHan/Interview_Question_for_Beginner
github.com
